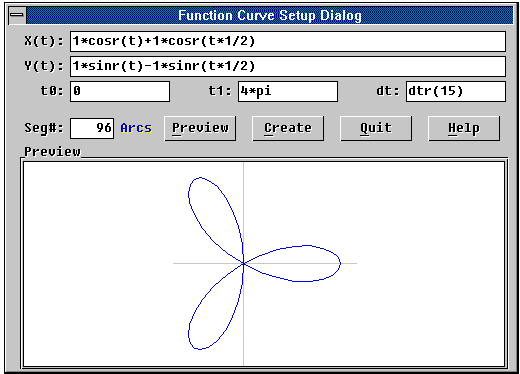
The FNCURVE command lets you realize a plane curve defined by a mathematic function in the parametric form: P(X(t),Y(t)), where X(t) and Y(t) are functions that evaluate the X and Y coordinates of a point on the curve at a specific value of t. The function curve will be realized only in the given range from t0 to t1, where

P(X(t0),Y(t0)) is the start point and P(X(t1),Y(t1)) is the end point of the resulted function curve segment.

Defining the Function Curve

Upon activation, the FNCURVE command will pop up a dialog window as shown in the figure below:

You must supply the correct data to the following text entry fields:

X(t)     Definition of the X ordinate function, must be given in TCL expression using parameter t as the only variable.

Y(t)     Definition of the Y ordinate function, must be given in TCL expression using parameter t as the only variable, such as the expression "t*sinr(t)".

t0     Start value of parameter t, can be given in TCL expression, such as "-2*pi".

t1     End value of parameter t, can be given in TCL expression, such as "-2*pi".

Dt     Sampling increment of parameter t, can be given in TCL expression, such as "dtr(5)" which means to evaluate the function points by every 5 ?

Preview of the Function Curve

Once these above text entry fields have contained correct function curve definition data, you may press the [Preview] button to see a preview image of the curve from the preview window. FNCURVE will automatically adjust the graphic extent to cover the whole curve in the given range and draw out the X and Y axis in gray color for reference.

There is a segment counter, beside the [Preview] button, which gives the required number of entities to realize the curve under current setting. It will be updated only when the preview image is generated.

Realization of the Function Curve

You may choose to realize the function curve by

• Creating Point entities on successively evaluated function points, or
• Creating Line segments connecting each successively evaluated function points, or
• Cubic spline fitting over the successively evaluated function points and resulting a smooth polyline containing arc segments.

You may specify the method by picking at the counter unit, which will toggle in the sequence "Pnts", "Lines" and "Arcs" for the above three methods respectively.

If the preview image gives correct result and the required segment counts is also acceptable, you may press the [Create] button to create the function curve in the drawing. The function definition data will also be listed out in the command area for latter reference.

Note that FNCURVE will always place the function curve's coordinate origin at the drawing's model space origin and the reference axis lines will not be created as seen from the preview image.

Exit of FNCURVE

FNCURVE will exit when you

• Press the [Create] button to create the curve and the curve is generated, or
• Press the [Quit] button, or
• Press <ESC> key or right mouse button.

FNCURVE will save the latest function curve definition data to disk file "FNCURVE.SET" at exit and restore it back at next command execution.

Special Notes

FNCURVE dose not check to see if the TCL expressions for the function definition are syntactically correct or not, nor does it analyze the expressions and give any active warning message about any sort of error. What it does is to pass these expressions to the TCL interpreter for execution. If there is anything wrong, the TCL interpreter will complain it and post appropriate error messages in the command area. You must justify the result by yourself from doing the preview of the function curve before creating it in the drawing.

FNCURVE does not check the continuity of the function within the given range. It simply evaluates the function points for every increment of the parameter t. If you choose to generate the curve using line or arc segments, FNCURVE will assume the function is continuous in the partition defined by any two successive function points evaluated and make the connection between them. You may need to edit the resulting curve if there should be any discontinuity of the curve in the given range. An example of such function curve is the Tangent function.

The generation of the function curve may be stopped at a point where a mathematic error is encountered in evaluating the TCL expression. It may be a singular point of the function or the value of the parameter t is out off the valid range. You will have to justify that by yourself.